Net Present Value Basics
To continue with our previous example, let's assume our investor wanted to know the delta between the $5MM purchase price and the price he would pay at his 8% discount rate . What he wants to know is the Net Present Value of this asset if he were to buy it at $5MM with an 8% discount rate on the future cash flows. To do this, let's start with our original PV formula:
From here, we simply add the purchase price as a negative number to the right hand side of the formula and the result will be the NPV.
So, what we are doing here is (1) discounting back the cash flow at an 8% to get the price our investor would be willing to pay to receive an 8% IRR and then (2) we are subtracting the purchase price that he was told he would have to pay to purchase the asset from that number.
Solving for NPV Formulaically
Let's solve for the NPV for our investor using his desired 8% discount rate. Below is how we solve formulaically and in the video we walk you through how to do this in Excel.
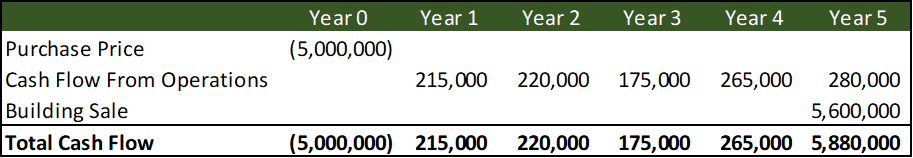
Thus to solve for NV formulaically:
Step 1.
Answer
Solving for NPV in Excel
In the video below we will walk through our example above using the =NPV() formula and discuss a bit more about Net Present Value and what happens with a different investor that has a different discount rate.
- Click here to download the Excel file used in the video.



Important note about the Excel NPV function: We don't include the purchase price in the NPV formula because the Excel NPV() function assumes the first amount included happens a year in the future. If we were to include the $5MM in the formula, it would assume that that was paid a year out and would discount it accordingly, which would be incorrect.)
The NPV Formula and IRR
Although there is no resulting difference, a lot of people think about the IRR in the context of the NPV formula and not the PV formula we learned earlier. Earlier, we solved for the IRR with the PV formula:
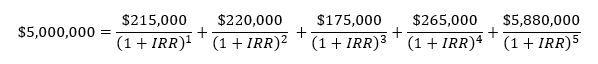
In this case, we simply subtract the sale price from both sides and solve for the IRR using an NPV of zero, which provides the same result.
However, in the industry, when you ask people to explain the IRR, many times you may hear that 'it is the discount rate that is applied to the future cash flow so that the NPV equals zero' rather than 'it is the discount rate applied to future cash flows so that the PV of the future cash flows equal the purchase price'. Both would be correct.